BELAJAR GITAR

Belajar gitar untuk pemula. Tadi anak - anak yang rewel mau di ajarin tinggal kunjungi blog saya ok.

Jika kuncinya agak gak kelihatan buka dimbah google. Tambahan ! tadi lupa bilang jari telunjuk harus selalu

di pinggir kiri sendiri. Untuk kunci - kunci yang lain saya posting di halaman judul yang sama ini. Good luck

NOVEL - NOVEL

 DEMIKIAN NOVEL - NOVEL YANG MUNGKIN MEMBANTU ANDA UNTUK MENCARI NOVEL YANG ANDA INGINKAN

 City of Thieves – David Benioff

Sepotong peristiwa yang menjadi bagian sejarah Perang Dunia II (1939-1945) adalah pengepungan kota Leningrad (sekarang dikenal dengan nama St. Petersburg) di Rusia yang dilakukan oleh Jerman, berlangsung selama kurang lebih 900 hari, dari tanggal 8 September 1941 hingga 8 Januari 1944. Pengepungan ini merupakan pengepungan terbesar dan paling berdarah dalam sejarah, menewaskan lebih dari 1 juta orang. Pihak Jerman menyebutnya Operation Nordlicht (Operasi Cahaya Utara).

Peristiwa sejarah inilah yang menjadi latar belakang cerita dalam novel Kota Para Pencuri (City of Thieves). Namun jangan bayangkan City of Thieves sebagai sebuah novel yang serius dan melankolis. Sang penulis, David Benioff, yang sejatinya adalah seorang penulis skenario film, mengambil sisi petualangan yang dialami tokoh-tokoh utama di tengah-tengah gejolak perang.

Pengeboman di kota Leningrad, gambar dari http://planetcoh.gamespy.com/

Benioff bercerita tentang sang ayah, yang konon telah membunuh dua orang Jerman sebelum ia berusia delapan belas tahun. Suatu hari sang ayah membeberkan segala ceritanya kepada Benioff, mengenai apa yang dialaminya semasa perang.

Adalah Lev, seorang pemuda Yahudi 17 tahun bertubuh pendek yang tinggal di apartemen yang dinamai Kirov, di salah satu sudut kota Leningrad. Ayah Lev yang seorang penyair  telah tewas di tangan Jerman, sementara ibu dan adik perempuannya mengungsi ke Moskwa. Tinggallah Lev dan teman-teman seapartemennya, anak-anak Piter (sebutan penduduk St. Petersburg bagi kota mereka) yang bangga, ikut berjuang mempertahankan kota.

Pada suatu malam yang membeku sesudah tahun baru, mayat seorang prajurit Jerman yang mati kedinginan melayang turun dengan parasutnya di atap Kirov. Lev mengambil pisau milik si prajurit, sementara teman-temannya mengambili barang-barang milik si prajurit yang lain. Siapa sangka lewat kejadian itu Lev akhirnya tertangkap oleh NKVD dan dijebloskan ke penjara Kresty. Di Kresty, Lev yang mengira bahwa hidupnya tidak akan lama lagi, bertemu dengan Kolya, seorang prajurit Rusia berumur awal dua puluhan yang punya ketampanan khas ras Arya: rambut berwarna jerami, mata biru, tubuh tinggi dan gagah. Kolya dijebloskan ke Kresty dengan tuduhan sebagai desertir. Tak disangka, mereka berdua malah dipertemukan dengan seorang kolonel tua yang akan melangsungkan pernikahan anak perempuannya dalam sepekan kedepan. Lev dan Kolya dibebankan suatu misi yang kedengarannya konyol namun taruhannya nyawa: mereka harus mencari selusin telur untuk kue pernikahan anak perempuan sang kolonel dalam waktu satu minggu!

Dari sini banyak petualangan yang dialami Lev dan Kolya, dan kebanyakan nyawa mereka hampir melayang dalam petualangan yang mereka jalani untuk mencari selusin telur. Saya tidak akan membocorkan apa saja yang mereka alami, anda harus membacanya sendiri :-p. Berhasilkah mereka memenuhi misi gila yang dipercayakan sang kolonel kepada mereka?

Satu hal yang tertanam di benak saya ketika membaca buku ini adalah: saya sungguh-sungguh bersyukur bahwa saya tidak hidup di tengah-tengah situasi perang. Benioff menggambarkan situasi yang terjadi saat itu dengan blak-blakan dan sangat riil, kekejaman dan kebrutalannya terasa banget, namun di saat yang sama juga menyorot hal-hal yang agak vulgar namun sangat manusiawi. Misalnya, Lev yang nggak pede tapi sangat penasaran dengan makhluk bernama cewek. Kolya, di sisi lain, adalah karakter yang suka omong besar, nekat, dan sebenarnya seorang maniak seks. Sangat menarik mengikuti perkembangan hubungan antara Lev dan Kolya, yang mana awalnya Lev sangat sebal dengan Kolya namun lama-lama mereka pun bersahabat.

Beberapa hal menarik yang saya temukan dalam buku ini:

Di halaman 104:

“Anak itu menjual sesuatu yg dijuluki orang permen perpustakaan. Cara membuatnya adalah dengan menghancurkan sampul buku, mengelupaskan lem perekatnya, lalu merebus, dan mencetaknya menjadi potongan-potongan yang selanjutnya dibungkus dlm kertas. Rasanya seperti lilin, tapi lem yang terkandung di dalamnya mengandung protein yg membuatmu tetap hidup. Sementara itu buku-buku di kota menghilang seperti burung dara.”

Baru tahu kan ada yang namanya permen perpustakaan? Saking sengsaranya orang-orang yang hidup di masa dan di tempat yang sedang terjadi peperangan, mereka sehari-hari hanya makan bawang dan roti yang sangat keras. Mereka menjadi sangat kurus dan banyak yang mati akibat kelaparan dan kedinginan (musim dingin di Rusia bisa mencapai titik suhu minus 30 derajat Celcius!) Jangankan telur dan daging, ”permen perpustakaan” ini merupakan hidangan yang cukup mewah bagi mereka! :-S

Di halaman 202:

“Tapi tak ada Elba untuk Hitler!”

Pulau Elba di Italia adalah tempat dimana Napoleon Bonaparte pernah dibuang. Ini kejutan yang saya suka dalam sebuah novel fiksi sejarah. I just love how the author can connect to another historical event. ;)

Just a warning: City of Thieves adalah novel dewasa. Saya tidak menyarankan siapapun yang berumur di bawah 18 tahun untuk membacanya.

Warm Bodies (Movie Cover)

“R” adalah zombi. Dia tidak punya ingatan, tidak punya identitas, dan tidak punya denyut nadi. Tetapi, dia punya mimpi. Dia tidak suka membunuh manusia. Dia agak berbeda dengan teman-temannya “Kaum Mati”. Sewaktu menjelajahi reruntuhan peradaban untuk mencari makan, R bertemu seorang gadis bernama Julie. Gadis itu merupakan kebalikan dari segala yang R tahu. Julie, yang hangat dan ceria serta sangat hidup, membuat sesuatu dalam diri R mulai berubah. R sadar dia tidak ingin memakan Julie, meski gadis itu tampak lezat. Dia ingin melindungi Julie, tak peduli apa pun akibatnya. Pilihan ini seperti percik api di rumput, melanggar aturan dan menyangkal logika, tetapi R tidak puas lagi dengan kehidupan dalam kematian. Dia ingin bernapas lagi, ingin hidup, dan Julie ingin membantunya. Bisakah kasih dari dua dunia yang berbeda ini berpadu?

Assasin Creed Revelation by Oliver Bowden

Perpustakaan Ordo Assassin tidak hanya menyimpan pengetahuan, tapi juga rahasia paling mengkhawatirkan yang pernah ada di dunia, rahasia yang Templar ingin gunakan untuk mengendalikan nasib manusia. Lima kunci diperlukan untuk membuka perpustakaan itu. Ezio harus pergi ke kota Konstantinopel yang penuh masalah, tempat tentara Templar dengan jumlahnya yang bertambah banyak mengancam untuk mengacaukan Kekaisaran Ottoman. Dengan menapaktilas pendahulunya, Altaïr, Ezio harus mengalahkan Templar untuk kali terakhir. Risikonya belum pernah segawat ini, dan perjalanan yang semula sekadar ziarah telah menjadi perpacuan melawan waktu...

Blood Rivals: Robert Pattinson & Taylor Lautners Biografi by Martin Howden

Dua bintang populer The Twilight Saga, Robert Pattinson dan Taylor Lautner beradu dalam biografi ganda unik ini. Dimulai dengan masa kecilnya di London, debut Robert Pattinson sebagai Cedric Diggory dalam film Harry Potter and Goblet of Fire. Pattinson kemudian berperan sebagai Edward Cullen dalam film Twilight. Twilight Saga dengan cepat menjadi fenomena global, dan mengangkat Robert menjadi bintang terpanas di Hollywood. Kemudian, juga mengikuti kehidupan remaja yang akan menjadi rival Pattinson, Taylor Lautner. Biografi ini menunjukkan bagaimana perannya sebagai Jacob Black dalam Twilight Saga telah mengubah dirinya menjadi bintang pujaan remaja internasional.

My Direction karya Narnie January

“Katakan yang sebenarnya. Aku sudah tidak tahan, Aurora.”
         Aurora mengangkat wajahnya, menatap Zayn penuh tanya. Gadis itu sama sekali tak memahami maksud kata-kata Zayn. 
       “Kau tidak perlu berpura-pura bodoh,” Zayn berbicara dengan nada yang lebih tinggi, namun lantas menginsyafi keberadaan Niall yang terlelap di dekat mereka berdua. “Katakan kenapa kau membuangnya?” 

Aurora masih tak memahami benda apa yang membuat cinta monyetnya semasa SMP, Zayn Malik, marah kepadanya. Bahkan hingga tiga tahun berlalu, saat mereka dipertemukan kembali dalam keadaan yang berbeda, di mana Zayn telah menjadi satu dari lima anggota boyband ternama One Direction.
         Cinta itu masih bersemi di hati yang terdalam, Zayn berupaya merebut kembali hati Aurora yang justru memilih untuk menjauh darinya dan terjebak dalam permainan dengan Niall Horan. Niall dibuat bingung oleh perasaannya kepada Aurora dan perasaan Aurora kepadanya. Belum lagi dengan tingkah Liam dan Harry yang terus mendesaknya untuk mendekati Aurora. Sementara itu, Zayn meminta Louis untuk menjadi penasihat cintanya supaya dia bisa kembali bersama Aurora.
           Aurora dilanda gelisah dan perasaan dosa. Gadis itu tidak bisa memahami dirinya sendiri, berusaha untuk mengambil sikap tapi setiap hal yang dia lakukan selalu saja disadarinya sebagai sebuah kesalahan. Dia ingin menjadi seseorang yang lebih baik. Dan, sikapnya ini semakin mempersulit Zayn untuk mendekatinya. Bagaimana akhir kisah cinta yang penuh rahasia satu sama lain ini?

Penulis: Aleya Aneesa
Penerbit: Alaf21
Tahun Pertama Terbit: 2006
Jumlah Halaman: 528



Novel yang satu ini termasuk karya fiksi yang populer di Malaysia. Novel ini berkisah seputar lika-liku kehidupan cinta seorang wanita bernama Emelda. Ia menikah dengan seorang pria bernama Aril Fatah. Pernikahan ini tidak didasarkan cinta melainkan sebuah keterpaksaan. Emelda terpaksa mengakui anak kembar kakaknya bernama Emira. Emira ini dihamili oleh Aril Fatah. Hanya saja ia kemudian meninggalkan Emira menanggung malu sendiri. Atas kejadian tersebut, Emira terguncang jiwanya, sakit dan sekarat. Atas paksaan beberapa orang, akhirnya Emelda memustuskan untuk mananggung malu Emira dengan mengakui anak kembar kakaknya sebagai anaknya. Kedua anak kembar tersebut bernama Atiea dan Dania. 8 Tahun sesudahnya, Aril Fatah kembali dan berpikir bahwa Emelda lah perempuan yang ia tiduri bertahun-tahun silam. Ia kemudian memaksa Emelda untuk menikah.

Penulis: Khrisna Pabichara
Penerbit: Noura Books (PT Mizan Publika)
Tahun Pertama Terbit: 2013
Jumlah Halaman: 378

Bagi setiap perantau sepertiku, rindu adalah hantu yang paling menakutkan. Tak ada yang tahu bagaimana ia mendatangiku setiap waktu.… begitu menyiksa, menggeretakkan tulang-tulang ketabahan.

Kalimat indah di atas merupakan penggalan perasaan Dahlan muda yang merindu keluarga di tengah perantauannya di Samarinda, Kalimantan. Dahlan memang melanjutkan kuliahnya di kota tersebut. Ia ingin membahagiakan Ayahnya juga menganggupi keinginan Aisa agar mereka kelak bertemu setelah berhasil meraih gelar sarjana. Dahlan menlanjutkan kuliah di PTAI Samarinda. Sebuah tempat yang tadinya ia anggap akan mengisi pengetahuan ke kepalanya. Tapi harapan Dahlan jauh meleset. Ia merasa apa yang diajarkan di kampusnya hanya sekedar teori. Karena sering merasa bosan, ia kemudian lebih sering meninggalkan kelas dan memilih pergi ke ruangan Pelajar Islam Indonesia (PII). Ia memang sangat aktif di organisasi tersebut


Kadang, kita mencintai seseorang begitu rupa sampai tidak menyisakan tempat bagi yang lain.
Membuat kita lupa untuk sekedar bertanya, inikah sebenarnya cinta?

Seperti itulah dia. Diam-diam mencintai lelaki itu dengan sangat dan menyimpan sakit tak berperih saat harus mendatangi pertunangannya dengan perempuan lain. Sedikit pun dia tak berniat menyesali atau berhenti mencintai lelaki itu.

Bukankah memang begitu cinta seharusnya? Memberikan senyum untuk dia yang kita cinta meski diam-diam menumpuk sedih sangat banyak di dalam hati. Dia yakin, seperti itulah cinta. Namun, saat semua berbalas, keraguan justru menjelma. Seperti inikah cinta yang selama ini dia tunggu?

Rumus Rumus Matematika SMP Kelas 9

Rumus Kesebangunan

Rumus-rumus kesebangunan sangat dibutuhkan dalam geometri, baik bidang datar maupun bangun ruang. Rumus kesebangunan ini juga mendasari ilmu trigonometri. Dengan demikian sangat penting bagi kita untuk mengingat rumus kesebangunan ini. Berikut ini aalah rumus-rumus kesebangunan

Dua bangun dikatakan sebangun jika
a. panjang sisi-sisi yang bersesuaian dari kedua bangun tersebut memiliki perbandingan senilai
b. sudut-sudut yang bersesuaian dari kedua bangun tersebut sama besar.
2. Bangun-bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen.
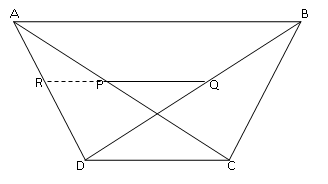
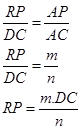
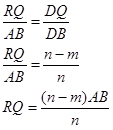
3. Syarat dua segitiga sebangun adalah sisi-sisi yang bersesuaian sebanding atau sudut-sudut yang bersesuaian sama besar.
4. Syarat dua segitiga kongruen:
a. Sisi-sisi yang bersesuaian sama panjang (s.s.s)
b. Dua sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar (s.sd.s)
c. Dua sudut yang bersesuaian sama besar dan sisi yang berada di antaranya sama panjang (sd.s.sd)
d. Dua sudut yang bersesuaian sama besar dan sisi yang berada di hadapannya sama panjang (sd.sd.s).

Yang pertama : untuk kasus siku-siku
Yang kedua : untuk segitiga sembarang

Penurunan rumus kesebangunan

 
Berapa panjang PQ jika AB (sisi yang panjang) dan DC (sisi yang pendek) diketahui panjangnya dan perbandingan AP : AC = BQ : BD diketahui.

Jawabannya ADA, simaklah ulasan berikut ini! Langsung aja ke TKP. hehehe

Pada posting sebelumnya, House of Math sudah mengulas cara menyelesaikan soal tersebut. Namun cara yang digunakan lumayan panjang. Nah sekarang House of Math akan mengulas tentang rumus cepat untuk menyelesaikan soal tersebut.
Dengan menggunakan proses berfikir pada posting pembahasan soal tersebut, kita bisa menurunkan rumus cepatnya.  Inilah caranya:

1.   Kita buat perpanjangan garis  PQ di R


2.   Misal = AP : AC = BQ : BD = m : n

3.   Selanjutnya Pandang segitiga ADC

Berlaku hubungan:


4.   Pandang segitiga ABD


Berlaku hubungan:


5.   RQ merupakan sebuah garis yang dapat dibentuk olah garis RP dan garis RQ sehingga:

6.   Sehingga untuk menghitung panjang PQ dapat langsung menggunakan rumus :

Dengan:
AB = sisi yang panjang
DC = sisi yang pendek
m : n = perbandingan letak P dan Q (kecil : besar)
Sekian penurunan rumus cepatnya, sepanjang itu menghasilkan rumus yang singkat,yang cepat, yang memudahkan pengerjaan soal. 

Peluang

Peluang, Permutasi & Kombinasi Matematika

Rumus Web mengumpulkan materi Peluang, Permutasi & Kombinasi Matematika ini untuk anak SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan dipelajari

1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga
Permutasi k unsur dari n unsur adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis atau .
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi

dengan penulisan nPk, hitung 10P4
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri

Contoh permutasi siklis :

Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :

2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,
Contoh :
Diketahui himpunan .
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :

Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).

Cara cepat mengerjakan soal kombinasi

dengan penulisan nCk, hitung 10C4

kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri
Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!

Peluang Matematika

1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.

Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}

2. Pengertian Peluang Suatu Kejadian
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :

Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3

3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).

Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :

Frekuensi harapan munculnya mata dadu 1 adalah

5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :

Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).

Peluang Kejadian Majemuk

1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :
Catatan : dibaca “ Kejadian A atau B dan dibaca “Kejadian A dan B”

Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :

2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku Jika . Sehingga Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika adalah peluang terjadinya A dan B, maka Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:

Sebaran Peluang

1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap dan setiap maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :

2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :

Dengan P sebagai parameter dan
Rumus ini dinyatakan sebagai:
untuk n = 0, 1, 2, …. ,n
Dengan P sebagai parameter dan
P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gaga